【讨论】FPGA设计中几种沿触发的用法及其优缺点【有图】

因为思念谁 · 发表于 2016-6-17 16:08:38

在数字系统设计中，经常涉及到要在某个时钟的上升沿或下降沿进行数据处理，通过自己总结和看别人的程序，发现有好多种方法进行处理，现在我把这几种方法列举一下，大家讨论下他们的优缺点。

背景：假设初始条件A=0，B=0，要在信号A的上升沿将B置为1。

方法1 最简单也是最容易想到的

module Test(rst_n, A, B);
input rst_n;
input A;
output B;
reg B;
always @(posedge A or negedge rst_n)
      if(!rst_n)
            B <= 1'b0;
      else
            B <= 1'b1;
endmodule

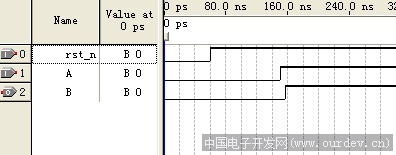
方法1仿真波形 (原文件名:m1.png)

方法2 通过系统时钟
module Test(rst_n,clock, A, B);

input rst_n;
input clock;
input A;
output B;

reg B;

reg A_BUF,A_RISE;

always @(posedge clock or negedge rst_n)
      if(!rst_n)
      begin
            A_BUF <= 1'b0;
            A_RISE <= 1'b0;
      end
      else
      begin
            A_BUF <= A;
            A_RISE <= (~A_BUF) & A;
      end

always @ (posedge clock or negedge rst_n)
      if(!rst_n)
            B <= 1'b0;
      else if(A_RISE)
                     B <= 1'b1;
endmodule

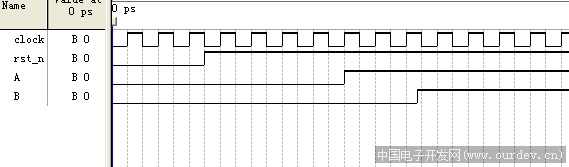
方法2仿真波形 (原文件名:m2.png)

方法3 跟方法2很像，结果却不太一样
module Test(rst_n,clock, A, B);

input rst_n;
input clock;
input A;
output B;

reg B;

reg A_BUF;

always @(posedge clock or negedge rst_n)
      if(!rst_n)
      begin
            A_BUF <= 1'b0;
      end
      else
      begin
            A_BUF <= A;
      end

wire A_RISE = (~A_BUF) & A;
always @ (posedge clock or negedge rst_n)
      if(!rst_n)
            B <= 1'b0;
      else if(A_RISE)
                     B <= 1'b1;
endmodule

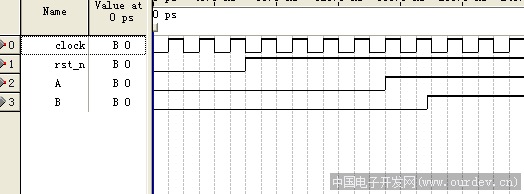
方法3仿真波形 (原文件名:m3.png)

方法4 使用系统时钟
module Test(rst_n,clock, A, B);

input rst_n;
input clock;
input A;
output B;

reg B;

reg[2:0] A_BUF;

always @(posedge clock or negedge rst_n)
      if(!rst_n)
      begin
            A_BUF <= 3'b000;
      end
      else
      begin
            A_BUF <= {A_BUF[1:0], A};
      end

wire A_RISE = (A_BUF[2:1] == 2'b01);

always @ (posedge clock or negedge rst_n)
      if(!rst_n)
            B <= 1'b0;
      else if(A_RISE)
                     B <= 1'b1;
endmodule

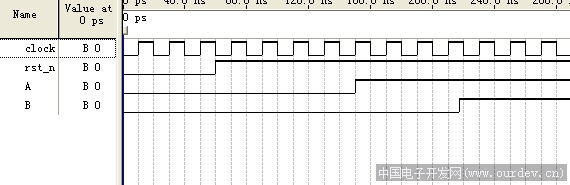
方法4仿真波形 (原文件名:m4.png)

目前我能想到的就这4种了，大家还有什么好的想法不妨一起交流下，呵呵

这些方法都能实现功能，只是反应时间上有区别。根据仿真结果来看，第一种结果最好，延时最短，但就是第一种我见到的用的最少，不知道为什么，这样用有什么缺点么？？？？