今天又发现一个关于完美洗牌的算法。这个比较简单一些,由 microsoft的Peiyush Jain提出。 ? 原论文: A Simple In-Place Algorithm for In-Shuffle. ? Peiyush Jain, Microsoft Corporation. ? July 2004 ? 问题描述: ? 所谓完美洗牌算法即是把输入为: ? a_1,a_2........a_n,b_1,b_2.........b_n的序列变为 ? b_1,a_1,b_2,a_2.......b_n,a_n 这是in perfect shufle。相对应的还有out perfect shuffle。两者区别在于首尾元素位置变或不变。 ? perfect shuffle算法要求在O(n),时间内,O(1)空间内完成。 ? perfect shuffle实质是一个置换。置换为: ? i -> 2*i mod (2*n+1) ? 由于置换可以分解为一系列不相交的轮换之积。故如果能找出所有轮换的一个代表元则可很容易解决问题。 ? 如 ? n=3时 输入 1 2 3 A B C b => A 1 B 2 C 3所对应的轮换为(1,2,4)(3,6,5) ? 选代表元为1和3以及一个临时变量T: ? 2->T,1->2 ? 1 2 3 A B C -----------> _ 1 3 A B C 4->1,T->4 _ 1 3 A B C -----------> A 1 3 2 B C ? 6->T,3->6 ? A 1 3 2 B C -----------> ?A 1 _ 2 B 3 5->3,T->5 ? A 1 _ 2 B 3 -----------> ?A 1 B 2 C 3 置换完成 ? 因此问题就转换为求置换的轮换分解中的代表元问题了。 ? 文中巧妙的利用特定条件下每个不相交的轮换可有3的不同幂次生成?。
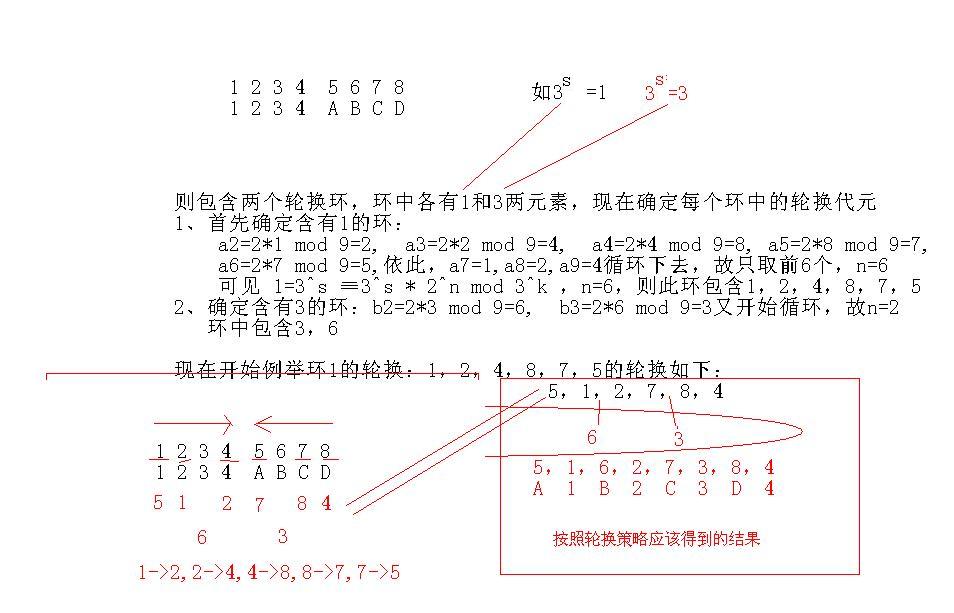
见论文:A Simple In-Place Algorithm for In-Shuffle. Peiyush Jain, Microsoft Corporation. 1、问题描述: 所谓完美洗牌算法即是把输入为: a_1,a_2........a_n,b_1,b_2.........b_n的序列变为 b_1,a_1,b_2,a_2.......b_n,a_n 这是in perfect shufle。 perfect shuffle算法要求在O(n),时间内,O(1)空间内完成。 perfect shuffle实质是一个置换。置换为: i -> 2*i mod (2*n+1) 由于置换可以分解为一系列不相交的轮换之积。故如果能找出所有轮换的一个代表元则可很容易解决问题。 如 len=3时 输入 1 2 3 A B C b => A 1 B 2 C 3所对应的轮换为(1,2,4)(3,6,5) 选代表元为1和3以及一个临时变量T: 1 2 3 A B C -----------> 2->T,1->2 _ 1 3 A B C -----------> 4->1,T->4 A 1 3 2 B C -----------> 6->T,3->6 A 1 _ 2 B 3 -----------> 5->3,T->5 A 1 B 2 C 3 置换完成 因此问题就转换为求置换的轮换分解中的代表元问题了。 文中巧妙的利用特定条件下: 即(2的任意次幂)对(3的k次幂)取模,能得到一个轮换环,并且环与环之间刚好互不相交 。 如我们分析长度2*n=3^k-1的置换的轮换分解。 (若长度为2*4=8,则8=3^2-1) 考虑某一包含3^s( 1 =< s < k )的轮换。不妨记3^s为a_1,3^k记为m。 则轮换里的数分别为: a_2 = 2* a_1 mod m a_3 = 2* a_2 mod m; a_4 = 2* a_3 mod m; 。。。。。 。。。 a_len = 2* a_len-1 mod m a_1 = 2* a_len mod m 则 a_1 ≡2^len * a_1 mod m; ( 最后一项中的a_len用倒数第二行乘2替代,以此类推........) , 依此,假设m=9,可以确定每个轮换中,len的值, 如a_1=3^s=3^0=1,则1=2^len * 1 mod m,则 len=2; 如a_1=3^s=3^1=3,则3=2^len * 3 mod m,则 len=6 因此每个3^s开始的一个轮换满足 : 3^s ≡3^s * 2^len mod 3^k ,且轮换的长度为len。 补充:若对1 2 3 4 5 6 7 8 9 10进行洗牌则首先交换成 1 2 3 4 6 7 8 9 5 10 (n=4,因此我们只对需要的前8个先调整到前面) 下面举了个例子:洗牌置换过程例证,它例举了将1234ABCD置换成A1B2C3D4的过程,请将图中的n理解为len,k=2。 |
[size=1em]1 [size=1em]2 [size=1em]3 [size=1em]4 [size=1em]5 [size=1em]6 [size=1em]7 [size=1em]8 [size=1em]9 [size=1em]10 [size=1em]11 [size=1em]12 [size=1em]13 [size=1em]14 [size=1em]15 [size=1em]16 [size=1em]17 [size=1em]18 [size=1em]19 [size=1em]20 [size=1em]21 [size=1em]22 [size=1em]23 [size=1em]24 [size=1em]25 [size=1em]26 [size=1em]27 [size=1em]28 [size=1em]29 [size=1em]30 [size=1em]31 [size=1em]32 [size=1em]33 [size=1em]34 [size=1em]35 [size=1em]36 [size=1em]37 [size=1em]38 [size=1em]39 [size=1em]40 [size=1em]41 [size=1em]42 [size=1em]43 [size=1em]44 [size=1em]45 [size=1em]46 [size=1em]47 [size=1em]48 [size=1em]49 [size=1em]50 [size=1em]51 [size=1em]52 [size=1em]53 [size=1em]54 [size=1em]55 [size=1em]56 [size=1em]57 [size=1em]58 [size=1em]59 [size=1em]60 [size=1em]61 [size=1em]62 [size=1em]63 [size=1em]64 [size=1em]65 [size=1em]66 [size=1em]67 [size=1em]68 [size=1em]69 [size=1em]70 [size=1em]71 [size=1em]72 [size=1em]73 [size=1em]74 [size=1em]75 [size=1em]76 [size=1em]77 [size=1em]78 [size=1em]79 [size=1em]80 [size=1em]81 [size=1em]82 [size=1em]83 [size=1em]84 [size=1em]85 [size=1em]86 [size=1em]87 [size=1em]88 [size=1em]89 [size=1em]90 [size=1em]91 [size=1em]92 [size=1em]93 [size=1em]94 [size=1em]95 [size=1em]96 [size=1em]97 [size=1em]98 [size=1em]99 | [size=1em][size=1em]#include "stdio.h" [size=1em]//轮换 [size=1em]void Cycle(int Data[],int Lenth,int Start) [size=1em]{ [size=1em] int Cur_index,Temp1,Temp2; [size=1em] [size=1em] Cur_index=(Start*2)%(Lenth+1); [size=1em] Temp1=Data[Cur_index-1]; [size=1em] Data[Cur_index-1]=Data[Start-1]; [size=1em] [size=1em] while(Cur_index!=Start) [size=1em] { [size=1em] Temp2=Data[(Cur_index*2)%(Lenth+1)-1]; [size=1em] Data[(Cur_index*2)%(Lenth+1)-1]=Temp1; [size=1em] Temp1=Temp2; [size=1em] Cur_index=(Cur_index*2)%(Lenth+1); [size=1em] } [size=1em]} [size=1em]//数组循环移位 参考编程珠玑 [size=1em]void Reverse(int Data[],int Len) [size=1em]{ [size=1em] int i,Temp; [size=1em] for(i=0;i<Len/2;i++) [size=1em] { [size=1em] Temp=Data; [size=1em] Data=Data[Len-i-1]; [size=1em] Data[Len-i-1]=Temp; [size=1em] } [size=1em]} [size=1em]void ShiftN(int Data[],int Len,int N) [size=1em]{ [size=1em] Reverse(Data,Len-N); [size=1em] Reverse(&Data[Len-N],N); [size=1em] Reverse(Data,Len); [size=1em]} [size=1em]//满足Lenth=3^k-1的perfect shfulle的实现 [size=1em]void Perfect1(int Data[],int Lenth) [size=1em]{ [size=1em] int i=1; [size=1em] if(Lenth==2) [size=1em] { [size=1em] i=Data[Lenth-1]; [size=1em] Data[Lenth-1]=Data[Lenth-2]; [size=1em] Data[Lenth-2]=i; [size=1em] return; [size=1em] } [size=1em] while(i<Lenth) [size=1em] { [size=1em] Cycle(Data,Lenth,i); [size=1em] i=i*3; [size=1em] } [size=1em]} [size=1em] //查找最接近N的3^k [size=1em]int LookUp(int N) [size=1em]{ [size=1em] int i=3; [size=1em] while(i<=N+1) i*=3; [size=1em] if(i>3) i=i/3; [size=1em] return i; [size=1em]} [size=1em]void perfect(int Data[],int Lenth) [size=1em]{ [size=1em] int i,startPos=0; [size=1em] while(startPos<Lenth) [size=1em] { [size=1em] i=LookUp(Lenth-startPos); [size=1em] ShiftN(&Data[startPos+(i-1)/2],(Lenth-startPos)/2,(i-1)/2); [size=1em] Perfect1(&Data[startPos],i-1); [size=1em] startPos+=(i-1); [size=1em] } [size=1em]} [size=1em]#define N 100 [size=1em] void main() [size=1em]{ [size=1em] int data[N]={0}; [size=1em] int i=0; [size=1em] int n; [size=1em] printf("please input the number of data you wanna to test(should less than 100):/n"); [size=1em] scanf("%d",&n); [size=1em] if(n&1) [size=1em] { [size=1em] printf("sorry,the number should be even "); [size=1em] return; [size=1em] } [size=1em] for(i=0;i<n;i++) [size=1em] data=i+1; [size=1em] perfect(data,n); [size=1em] for(i=0;i<n;i++) [size=1em] printf("%d ",data); [size=1em]} |
| 欢迎光临 中科因仑“3+1”工程特种兵精英论坛 (http://bbs.enlern.com/) | Powered by Discuz! X3.4 |